We apply Ampere's Law in integral form:
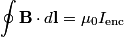 By symmetry, this can simplified to  Because the wire is hollow, equation (1) implies that 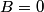 when when 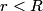 . .Let 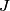 be the constant volume current density in the region be the constant volume current density in the region 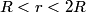 . Then, . Then,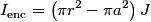 So, 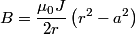 When 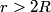 , , 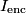 is constant and equal to is constant and equal to 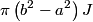 , so , so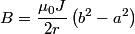 Only answer (E) shows the correct behavior for 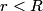 and and 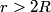 , therefore this answer is correct. , therefore this answer is correct. |