We first apply Snell's Law to the upper surface of the fiber and find the condition for total internal internal reflection.
Total internal reflection occurs when Snell's Law 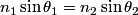 fails because of the fact that 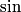 cannot be larger than cannot be larger than 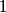 . If we take medium . If we take medium 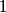 to be the optical fiber and medium to be the optical fiber and medium  to be free space, then to be free space, then 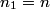 and and 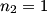 . So, Snell's Law will fail when . So, Snell's Law will fail when 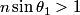 or 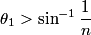 Now, from the right triangle in the diagram, we see that an application of Snell's Law to the leftmost surface of the fiber gives 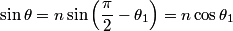 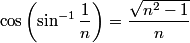 So, light will stay in the fiber when 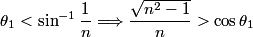 So, the condition for total internal reflection is 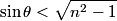 or 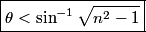 Therefore, answer (B) is correct. |