Gauss's Law states that
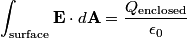 We are told that 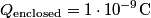 , so the total flux through the surface is , so the total flux through the surface is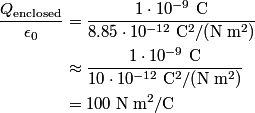 So, the flux through the rest of the surface is approximately 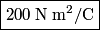 . Therefore, answer (E) is correct. . Therefore, answer (E) is correct. |
Gauss's Law states that
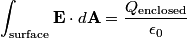 We are told that 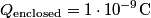 , so the total flux through the surface is , so the total flux through the surface is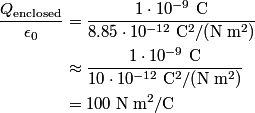 So, the flux through the rest of the surface is approximately 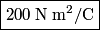 . Therefore, answer (E) is correct. . Therefore, answer (E) is correct. |