There are
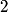 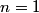 orbitals: orbitals: \begin{enumerate} \item \text{ 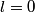 , , 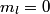 , , 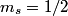 } }\item \text{ 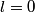 , , 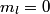 , , 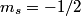 } }\end{enumerate} There are 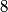 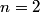 orbitals: orbitals:\begin{enumerate} \item \text{ 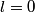 , , 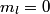 , , 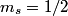 } }\item \text{ 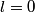 , , 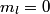 , , 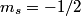 } }\item \text{ 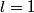 , , 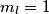 , , 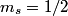 } }\item \text{ 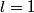 , , 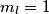 , , 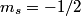 } }\item \text{ 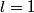 , , 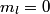 , , 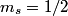 } }\item \text{ 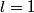 , , 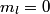 , , 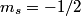 } }\item \text{ 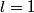 , , 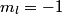 , , 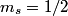 } }\item \text{ 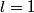 , , 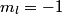 , , 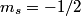 } }\end{enumerate} This makes a total of 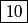 . Therefore, answer (E) is correct. . Therefore, answer (E) is correct. |