Recall that
 The two decay products must be back to back in order to conserve three momentum (the initial three momentum is 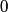 ). Let ). Let 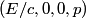 be the four-vector of the massless particle. Equation (1) with be the four-vector of the massless particle. Equation (1) with 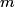 replaced by replaced by 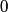 implies that implies that 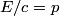 . So, the four-momentum of the massless particle is . So, the four-momentum of the massless particle is 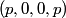 . By three-momentum conservation, the three-momentum of the massive particle must be . By three-momentum conservation, the three-momentum of the massive particle must be 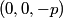 . From equation (1), the four-momentum must then be . From equation (1), the four-momentum must then be 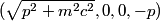 . The initial energy is . The initial energy is 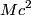 , so by energy conservation, , so by energy conservation,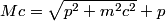 Squaring both sides and solving for 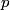 yields yields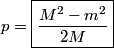 Therefore, answer (B) is correct. |