We use Faraday's Law in integral form
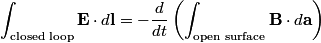 We choose to traverse the loop in a clockwise direction. We also choose the reference direction of the current 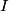 to be in the counter-clockwise direction. Then, to be in the counter-clockwise direction. Then,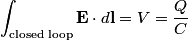 where 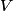 is the voltage difference between the upper left-hand corner of the circuit and the lower left-hand corner of the circuit and is the voltage difference between the upper left-hand corner of the circuit and the lower left-hand corner of the circuit and 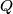 is the charge on the upper plate of the capacitor. Also, is the charge on the upper plate of the capacitor. Also,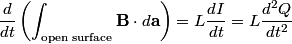 So, Faraday's Law is 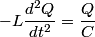 At 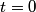 , , 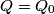 and and 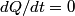 , so the solution to this equation is , so the solution to this equation is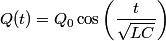 and 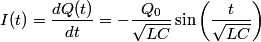 The energy stored in the inductor as a function of time is therefore 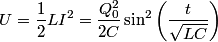 Thus, answer (A) is correct. |