The Carnot efficiency is
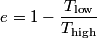 where 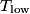 and and 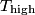 are the low and high temperatures in are the low and high temperatures in 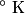 . So, in this case, . So, in this case,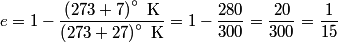 The efficiency is defined as the ratio of the work 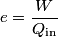 where 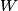 is the work done by the Carnot engine and is the work done by the Carnot engine and 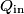 is the heat input to the engine. In this problem, the engine is being run in reverse as a heat pump, so the work is the heat input to the engine. In this problem, the engine is being run in reverse as a heat pump, so the work 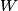 is the work done to the engine and the denominator of is the work done to the engine and the denominator of  is the heat output by the heat pump. is the heat output by the heat pump.So, the minimum amount of work required to put out 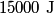 of heat is of heat is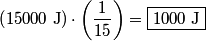 Therefore, answer (B) is correct. |