The weighted average of two independent measurements
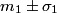 and and 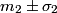 is defined as the value of is defined as the value of 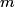 that maximizes the log likelihood function that maximizes the log likelihood function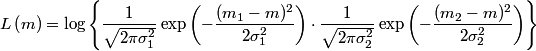 or minimizes the function 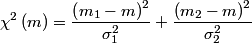 Taking the derivative of 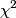 with respect to with respect to 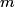 , setting it equal to , setting it equal to 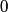 , and solving for , and solving for 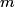 gives gives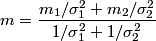 We use error propagation to find the error 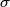 on on 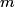 : :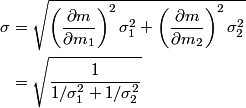 We are given that 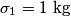 and and 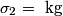 . Therefore, . Therefore, 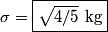 . Therefore, answer (B) is correct. . Therefore, answer (B) is correct. |