We apply conservation of (relativistic) energy and conservation of (relativistic) momentum. Let
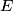 denote the energy of the photon that was destroyed. The initial momentum is denote the energy of the photon that was destroyed. The initial momentum is 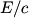 and the initial energy is and the initial energy is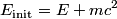 We are told that the positron and the two electrons move off with the same speed at the end. So, they must each have a momentum equal to 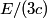 . Therefore, the total energy at the end is . Therefore, the total energy at the end is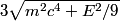 Equating the initial and final energies and then squaring both sides of the equation, we find that 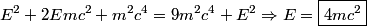 Therefore, answer (D) is correct. |