Snell's equation tells us that
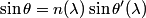 This implies that 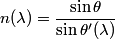 We differentiate this equation with respect to 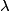 : :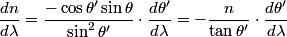 So, if the spread in the wavelength is 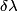 , then the spread in the angle of refraction is given by , then the spread in the angle of refraction is given by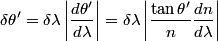 Therefore, answer (E) is correct. |
Snell's equation tells us that
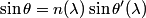 This implies that 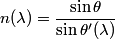 We differentiate this equation with respect to 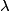 : :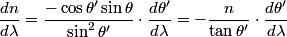 So, if the spread in the wavelength is 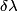 , then the spread in the angle of refraction is given by , then the spread in the angle of refraction is given by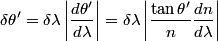 Therefore, answer (E) is correct. |