The probability that the electron is between
 and and 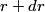 is is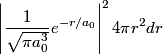 So, the probability is proportional to 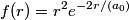 . We can find the maximum value of the probability by differentiating . We can find the maximum value of the probability by differentiating 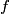 with respect to with respect to  and setting the derivative equal to and setting the derivative equal to 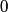 . .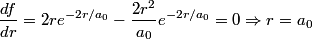 We can check that this is a local maximum by finding the second derivative 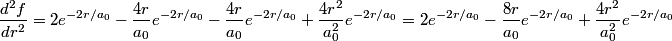 If we plug in 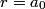 , we find that , we find that 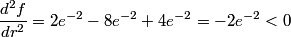 Therefore, 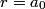 is indeed a local maximum of the radial probability density function. Therefore, the correct answer is is indeed a local maximum of the radial probability density function. Therefore, the correct answer is 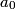 . . |