We use Faraday's Law in integral form
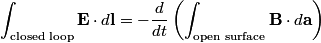 We choose to traverse the loop in such a way so that when the loop is in the position shown in the figure, the traversal appears clockwise when viewed as in the figure. We also choose the reference direction of the current 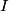 to be in the same direction as the traversal. Then to be in the same direction as the traversal. Then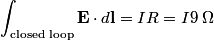 By the right-hand corkscrew rule, 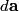 points in the points in the 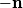 direction. Therefore, direction. Therefore, 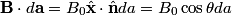 where where 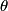 is the angle between is the angle between 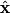 and the normal vector and the normal vector 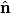 . We are given that . We are given that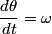 and that 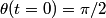 . Therefore, . Therefore, 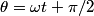 . Therefore, . Therefore, 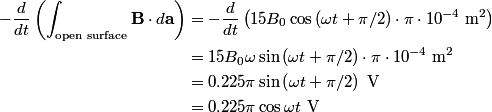 Therefore, 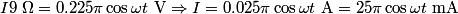 Note that the reference direction that we chose was actually the correct, because when 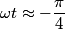 , so that the coil is in the orientation that is shown in the figure, then the current I is positive. Therefore, answer (E) is correct. , so that the coil is in the orientation that is shown in the figure, then the current I is positive. Therefore, answer (E) is correct. |