Recall the definition of resistance
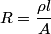 where 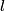 is the length of the wire, is the length of the wire, 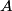 is the cross-sectional area of the wire, and is the cross-sectional area of the wire, and 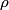 is the resistivity of the wire material. Let is the resistivity of the wire material. Let 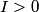 be the current that runs from the be the current that runs from the 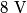 terminal to the terminal to the 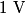 through the Nichrome wire. Then by Ohm's Law the following relationship must hold: through the Nichrome wire. Then by Ohm's Law the following relationship must hold: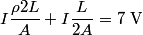 This implies that 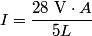 Therefore, the potential difference across the smaller wire is 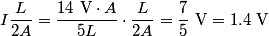 Therefore, the potential at the junction is 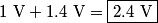 Therefore, answer (A) is correct. |