We use the velocity addition formula:
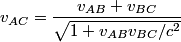 This formula can be derived directly from the Lorentz transformations, and therefore it does not only apply to particles with mass. It applies to paths through space parametrized by time that travel at less than or equal to the speed of light. Here 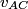 is the velocity of the path as seen in reference frame is the velocity of the path as seen in reference frame 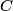 , , 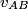 is the velocity of the path with respect to reference frame is the velocity of the path with respect to reference frame 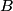 , and , and 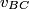 is the velocity of reference frame is the velocity of reference frame 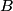 relative to reference frame relative to reference frame 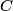 . . In the case of this problem, reference frame 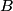 is the tube and reference frame is the tube and reference frame 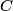 is the lab. So, is the lab. So, 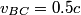 , , 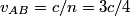 , so , so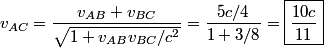 Therefore, answer (D) is correct. |