(A) The fact that energy is released in the fission process means that the end products are more stable that original uranium-
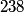 nucleus, so the reaction is energetically possible, and one cannot conclude that spontaneous fission cannot occur. nucleus, so the reaction is energetically possible, and one cannot conclude that spontaneous fission cannot occur.(B) A ``large neutron excess" does not really mean anything specific. (C) If the two equal fragments each had a mass greater than half that of 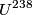 , then the total energy after the fission would be greater than the total energy before the fission. Conservation of energy implies that this is impossible, unless energy is somehow added to the system. But we are told that energy is actually released during the fission, not added, so answer (C) is wrong. , then the total energy after the fission would be greater than the total energy before the fission. Conservation of energy implies that this is impossible, unless energy is somehow added to the system. But we are told that energy is actually released during the fission, not added, so answer (C) is wrong.(D) and (E) We can calculate the binding energy per nucleon for the two equal fragments, which must have an atomic number near 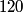 , as follows. The binding energy of a nucleus is defined as , as follows. The binding energy of a nucleus is defined as![\begin{align*}B = \left[N m_n + Z M({^1H}) - M\left({^A_ZX} \right) \right]c^2\end{align*} \begin{align*}B = \left[N m_n + Z M({^1H}) - M\left({^A_ZX} \right) \right]c^2\end{align*}](../images/609f80f3c3dbb5b3afcbb1d0ded51a11de6be1b1.gif) The initial binding energy is approximately 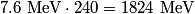 . The final binding energy is approximately . The final binding energy is approximately 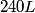 where where 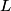 is the binding energy per nucleon for nuclei near is the binding energy per nucleon for nuclei near 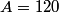 . The final binding energy minus the initial binding energy must equal the amount of energy released during the reaction. Therefore, . The final binding energy minus the initial binding energy must equal the amount of energy released during the reaction. Therefore,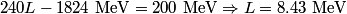 Therefore, answer (E) is correct. |