The two important experimental facts relating to the heat capacity of solids are (see Yoshioka page 67)
\begin{enumerate} \item ``Around room temperature, ordinary simple solids have a molar heat of about 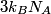 ... ...\item ``At low temperatures, the molar heat heat decreases in proportion to 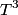 " "\end{enumerate} The Einstein model successfully reproduces the first experimental observation about the heat capacity at room temperature. However, the Einstein model FAILS to reproduce the 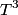 dependence at low temperatures. In the Einstein model, the heat capacity at low temperatures decreases EXPONENTIALLY instead of in proportion to dependence at low temperatures. In the Einstein model, the heat capacity at low temperatures decreases EXPONENTIALLY instead of in proportion to 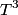 . The Debye model, on the other hand, successfully reproduces BOTH experimental observations. The answer to this question is therefore (D). . The Debye model, on the other hand, successfully reproduces BOTH experimental observations. The answer to this question is therefore (D). We can also arrive at answer (D) by directly taking the limit of the given molar heat capacity as the temperature goes to infinity. 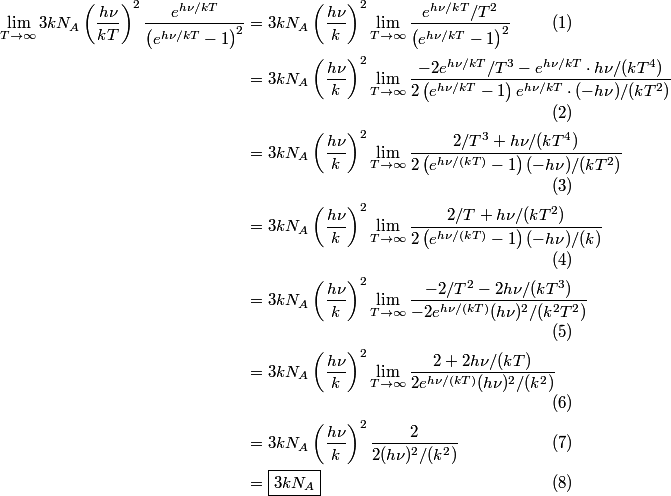 Therefore, answer (D) is correct. |