The cyclotron frequency is given in Hz, so we must assume it is not an angular frequency. The formula for the cyclotron frequency (not an angular frequency) is
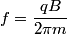 This can be derived as follows. The Lorentz force must equal the force required to maintain circular motion 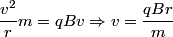 The frequency is then given by 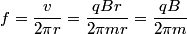 So, we solve for 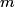 and plug in the given numbers and plug in the given numbers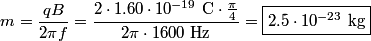 Therefore, answer (A) is correct. |