We are given the magnitude of the electric field vector as a function of time, but not its direction. In fact, we cannot know its direction, but we do know that it is in a plane parallel to the conductor's surface. This follows from the general formula for an electromagnetic plane wave propagating in the
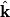 direction: direction: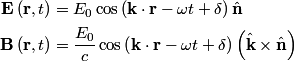 where 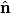 and and 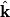 are orthogonal. In our case, we know that are orthogonal. In our case, we know that 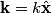 and that and that 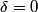 . Therefore, the above equations reduce to . Therefore, the above equations reduce to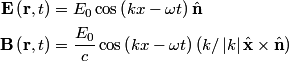 For the incoming wave 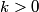 and for the reflected wave and for the reflected wave 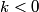 . The magnitude of . The magnitude of 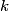 , which is determined by the speed of light in vacuum and the angular frequency , which is determined by the speed of light in vacuum and the angular frequency  must be the same for both the transmitted and the reflected waves, because must be the same for both the transmitted and the reflected waves, because  must be the same. must be the same. The boundary conditions for time-varying electric and magnetic fields at the surface of a perfect conductor are: 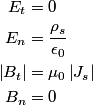 where 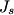 is the surface current density and is the surface current density and 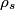 is the surface charge density. is the surface charge density. 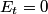 implies that the electric fields of the incident and reflected waves will be reversed. This implies implies that the electric fields of the incident and reflected waves will be reversed. This implies 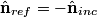 and that and that 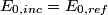 . The transverse component of the electric field in the reflected and the incident waves is the only component. So, because the transverse electric field vector is . The transverse component of the electric field in the reflected and the incident waves is the only component. So, because the transverse electric field vector is 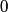 at at 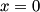 , the total electric field vector must also be zero at , the total electric field vector must also be zero at 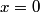 . The magnetic field vector of the reflected wave can be found using . The magnetic field vector of the reflected wave can be found using 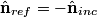 , , 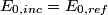 , and , and 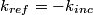 : :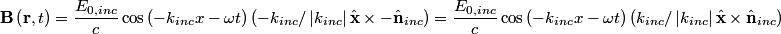 So, the magnetic field vector of the reflected wave is not reversed and the total magnetic field vector at 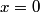 is simply two times the incident magnetic field vector evaluated at is simply two times the incident magnetic field vector evaluated at 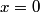 . Therefore, . Therefore,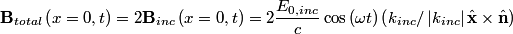 The magitude of the total magnetic field vector at 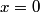 is therefore, is therefore,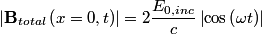 The notation of the problem uses 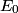 in place of in place of 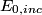 . So, to summarize the magnitudes of the total electric field and total magnetic field immediately to the left of the conductor are . So, to summarize the magnitudes of the total electric field and total magnetic field immediately to the left of the conductor are 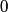 and and 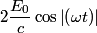 , respectively. This is very similar to the answer in (C), except the absolute value signs are missing there. Apparently, the answer in (C) is the component of the magnetic field vector in the , respectively. This is very similar to the answer in (C), except the absolute value signs are missing there. Apparently, the answer in (C) is the component of the magnetic field vector in the 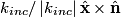 direction. Answer (C) is clearly the best one though, so it should be chosen. direction. Answer (C) is clearly the best one though, so it should be chosen. |