The force on the electron is given by the Lorentz equation
 The proton's velocity after being accelerated through a potential difference 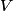 in the in the  direction is direction is We are told that the electric field is in the 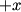 direction and that the magnetic field is in the direction and that the magnetic field is in the 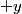 direction. Therefore, direction. Therefore,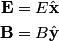 Because the proton's trajectory is unaffected, we set 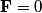 in equation (1). in equation (1). 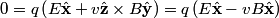 So, initially 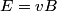 . But when the potential difference is increased by a factor of . But when the potential difference is increased by a factor of 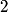 , ,  is increased by a factor of two (see equation (2)). Therefore, is increased by a factor of two (see equation (2)). Therefore, 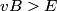 , so the particle is deflected in the , so the particle is deflected in the 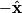 direction. Therefore, answer (B) is correct. direction. Therefore, answer (B) is correct. |