Use the formula
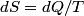 . Entropy is a state function, so if we compute the integral of . Entropy is a state function, so if we compute the integral of 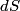 for a different process with the same initial and final states, the result should be the same. So, we choose a reversible isothermal expansion. The original process was adiabatic and involved no work done by the gas. So, the temperature of the gas cannot change. So, the initial and final temperatures are the same, so a reversible isothermal process will indeed have the same initial and final states as the actual process. For a reversible isothermal process, the internal energy of the gas does not change (because for a different process with the same initial and final states, the result should be the same. So, we choose a reversible isothermal expansion. The original process was adiabatic and involved no work done by the gas. So, the temperature of the gas cannot change. So, the initial and final temperatures are the same, so a reversible isothermal process will indeed have the same initial and final states as the actual process. For a reversible isothermal process, the internal energy of the gas does not change (because 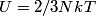 ). So, ). So, 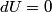 . Therefore, by the second law of thermodynamics . Therefore, by the second law of thermodynamics 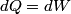 . Therefore, if we let . Therefore, if we let 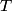 be the temperature of the gas (which does not change) and be the temperature of the gas (which does not change) and 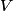 denote the initial volume of the gas, then denote the initial volume of the gas, then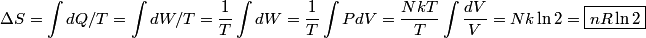 Therefore, answer (B) is correct. \section*{alternate solution:} Use the statistical definition of entropy, 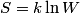 where where 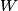 is the number of microscopic states of the system. We assume that the number of locations that each particle could be in (i.e. the number of single particle states) is proportional to the volume is the number of microscopic states of the system. We assume that the number of locations that each particle could be in (i.e. the number of single particle states) is proportional to the volume 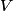 , i.e. , i.e. 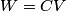 where where 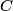 is a constant. Then the total number of states is given by is a constant. Then the total number of states is given by 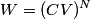 where where 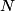 is the number of particles. Thus, is the number of particles. Thus,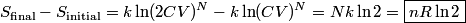 Therefore, answer (B) is correct. |