Initially, all of the energy in the system is gravitational. Just before the rod hits the ground, all of the gravitational energy is converted to kinetic energy, assuming we use the ground as the reference level of the potential energy. The initial potential energy is given
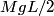 The final kinetic energy is given by 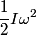 where 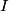 is the moment of inertia of the rod about the pivot point and is the moment of inertia of the rod about the pivot point and  is the angular velocity of the rod just before it strikes the ground. By the parallel axis theorem, is the angular velocity of the rod just before it strikes the ground. By the parallel axis theorem,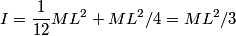 Therefore, 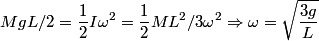 The speed of the free end just before it strikes the ground is then 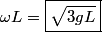 Therefore, answer (C) is correct. |