The potential is zero at the origin, so the particle will have kinetic energy equal to
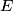 there. So, its velocity will be there. So, its velocity will be  . If the particle is moving to the right, then its acceleration will be . If the particle is moving to the right, then its acceleration will be 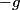 . The time it will take for the particle to come to rest is . The time it will take for the particle to come to rest is 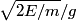 . Then the particle will start moving backward toward the origin. The time it will take to do that is also . Then the particle will start moving backward toward the origin. The time it will take to do that is also 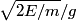 . So, the total time the particle spends on the right side of the . So, the total time the particle spends on the right side of the 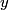 -axis is -axis is 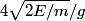 . .Now, assume the particle is at the origin and is moving to the left with velocity  . If the potential were . If the potential were 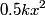 for for 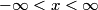 (instead of only (instead of only 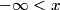 ), would also be at the origin and moving to the left with speed ), would also be at the origin and moving to the left with speed  at some point in time during its period. The period for the at some point in time during its period. The period for the 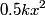 potential for potential for 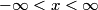 is is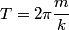 By symmetry, the particle spends half of its time to the left of the y-axis and half of its time to the right of the y-axis. So, the amount of time it spends to the left of the axis is 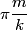 We add the amount of time the particle spends to the left of the y-axis to the amount of time the particle spends to the right of the  -axis to obtain the period: -axis to obtain the period: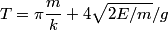 Therefore, answer (D) is correct. |