First we find the minimum of the potential.
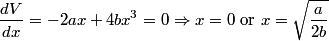 The second derivative of the potential is 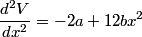 Plugging in 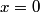 and and 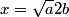 shows that shows that 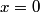 is a local maximum and is a local maximum and 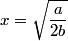 is a local minimum. So, we consider small oscillations about is a local minimum. So, we consider small oscillations about 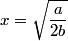 . Define . Define 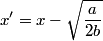 . We would like to know the force on the particle as a function of . We would like to know the force on the particle as a function of 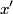 . This can be easily found as follows: . This can be easily found as follows: 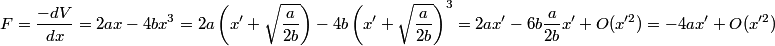 Since we are told to consider only small oscillations about the minimum, we can ignore that 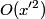 terms. The angular frequency of oscillations in the case where we have a spring with spring constant terms. The angular frequency of oscillations in the case where we have a spring with spring constant 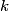 is is 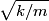 , so, by analogy, the angular frequency of oscillations here is: , so, by analogy, the angular frequency of oscillations here is: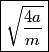 Therefore, answer (D) is correct. |