Let
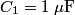 and and 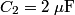 . Let . Let 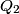 denote the charge on the positive side of the the denote the charge on the positive side of the the 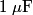 capacitor and let capacitor and let 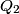 denote the charge on the positive side of the denote the charge on the positive side of the 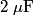 capacitor. Let capacitor. Let 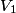 denote the voltage across the denote the voltage across the 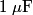 capacitor and let capacitor and let 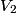 denote the voltage across the denote the voltage across the 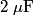 capacitor. Let capacitor. Let 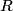 denote the total resistance of the wire (so R include the resistance from both of the two disconnected sections of the wire). denote the total resistance of the wire (so R include the resistance from both of the two disconnected sections of the wire).The current must be the same everywhere in the circuit. Therefore, the rate at which positive charges leave the 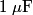 capacitor must equal the rate at which positive charges leave the capacitor must equal the rate at which positive charges leave the 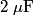 capacitor. That is capacitor. That is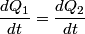 This implies that 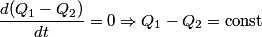 Initially, 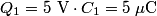 and and 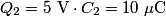 . So, . So, 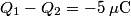 . .The current through the resistor must be zero when the circuit reaches a steady state, so the magnitudes of the voltages across the capacitors must be equal, and their sign must be opposite (because of Kirchhoff's voltage law). That is, 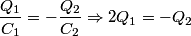 The solution to the system of equations 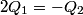 and and 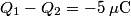 is is 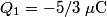 and and 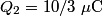 . .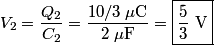 Therefore answer (C) is correct. |