The formula for the relativistic Doppler shift is
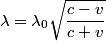 where the sign of  depends on whether the observer and the source are approaching or receding. In this problem, there are two sources, and one of them is receding and one of them is approaching, so the difference in wavelength is depends on whether the observer and the source are approaching or receding. In this problem, there are two sources, and one of them is receding and one of them is approaching, so the difference in wavelength is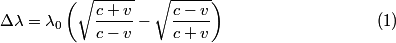 where now  is the speed (not the velocity) of a particle on the Sun's equator due to the Sun's rotation. Now, is the speed (not the velocity) of a particle on the Sun's equator due to the Sun's rotation. Now, 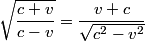 and 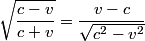 so, we can rewrite equation (1) as 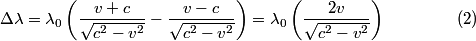 Now, we guess that the speed  is tiny compared to the speed of light. This is intuitive, because one normally does not think of relativistic speeds when one thinks of the Sun macroscopically. Thus, we set is tiny compared to the speed of light. This is intuitive, because one normally does not think of relativistic speeds when one thinks of the Sun macroscopically. Thus, we set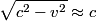 Then equation (2) becomes 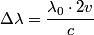 We are given 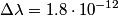 , , 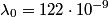 , so we can easily solve for , so we can easily solve for  . We find that . We find that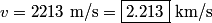 This is indeed a nonrelativistic speed, so the approximation that 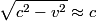 was a good one. Therefore, answer (B) is correct. was a good one. Therefore, answer (B) is correct. |