Setting
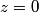 , , 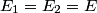 , and taking the real part of the given equation for the electric field vector, we find that , and taking the real part of the given equation for the electric field vector, we find that 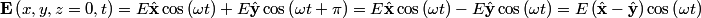 This describes a line that goes through the points 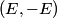 and and 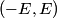 . Therefore, either answer a) or answer b) is correct. If the angles in answers a) and b) are the standard azimuthal angles, i.e. angles measured counterclockwise from the x-axis, then answer (B) is correct (but this is really not clear from the problem statement). . Therefore, either answer a) or answer b) is correct. If the angles in answers a) and b) are the standard azimuthal angles, i.e. angles measured counterclockwise from the x-axis, then answer (B) is correct (but this is really not clear from the problem statement). |