The half-life
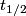 of a particle that decays according to of a particle that decays according to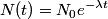 is defined as the time 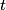 such that such that 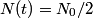 . Therefore, if half of the muons live to reach the detector, then the muons must have experienced a time of . Therefore, if half of the muons live to reach the detector, then the muons must have experienced a time of 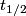 between their generation and their detection. between their generation and their detection.We use the time dilation formula to find the time between the generation and the detection of the muons in the laboratory frame: 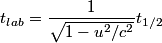 Therefore, 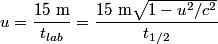 Squaring both sides and solving for 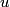 gives: gives: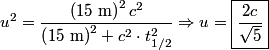 \section*{alternate solution:} Using the fact that the invariant interval between the generation and the detection of the muons must have the same value in both reference frames, we have 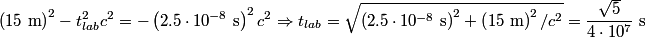 Therefore, the velocity in the lab frame is 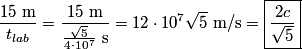 Therefore, answer (C) is correct. |