We evaluate the line integral using the following parametrization of the circular path
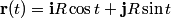 The derivative of 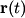 is is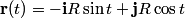 So, the line integral is 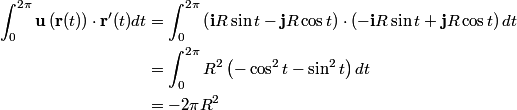 The problem statement does not tell us whether to traverse the circle clockwise or counterclockwise, so we assume that only the magnitude of the line integral is important. Therefore, (C) is the correct answer. |