We use the result of Problem 3. The force on a particle with charge
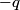 that is on the axis of symmetry is that is on the axis of symmetry is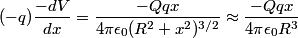 This follows from the fact that 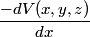 evaluated at 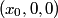 equals equals 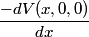 evaluated at 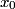 . . The angular frequency of oscillations in the case where we have a spring with spring constant k is 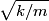 , so by analogy, the angular frequency of oscillations here is: , so by analogy, the angular frequency of oscillations here is: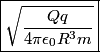 Therefore, answer (A) is correct. |