The spherical harmonics form an orthonormal basis, and the given state is normalized, so we can add up the probabilities that the the molecule is observed in each of the spherical harmonic states with total angular momentum
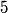 i.e. in each of the i.e. in each of the 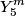 states. The probability to measure states. The probability to measure 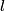 and and 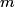 for the total angular momentum and the azimuthal angular momentum quantum number is for the total angular momentum and the azimuthal angular momentum quantum number is 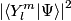 , so the desired probability is: , so the desired probability is: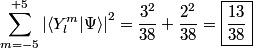 Therefore, answer (C) is correct. |