The formula for the electric potential of a localized charge distribution (with the convention that
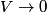 as the distance from the charge distribution goes to infinity) is as the distance from the charge distribution goes to infinity) is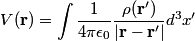 In the case of this problem 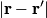 is always equal to is always equal to 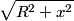 when the when the 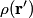 is nonzero. Thus, is nonzero. Thus, 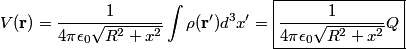 Therefore, answer (B) is correct. |