III. The adjoint of an operator
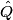 is the operator such is the operator such 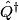  for all f and g. Using the well-known fact that the position operator and the momentum operator are Hermitian (they must be, since they are observables!), we have that 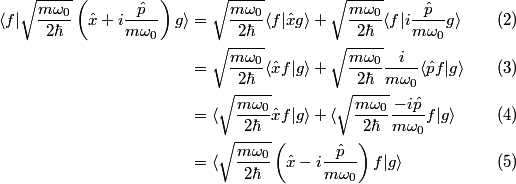 Thus, the operator 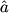 and its adjoint are different, so statement II is CORRECT. and its adjoint are different, so statement II is CORRECT.II. First of all, the fact that an operator is Hermitian does NOT imply that it represents observable. (The converse, however, is true: the fact that an operator represents an observable DOES imply that the operator is hermitian.) An operator 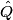 is Hermitian if and only if is Hermitian if and only if  for all f and g. If 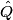 were Hermitian, then were Hermitian, then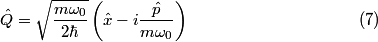 because of the work above and the fact that the Hermitian adjoint of an operator is unique. But equality is clearly NOT true, therefore, the assumption that 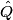 is Hermitian is false. is Hermitian is false. |