When the capacitor is charged, the voltage across it is equal to the voltage across the battery (
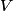 ). The voltage across a capacitor cannote change discontinuously, therefore the voltage across the capacitor immediately after the switch is thrown to contact ). The voltage across a capacitor cannote change discontinuously, therefore the voltage across the capacitor immediately after the switch is thrown to contact 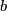 is still is still 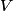 . We can apply Kirchhoff's voltage loop around the right loop to find that . We can apply Kirchhoff's voltage loop around the right loop to find that where 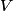 is the voltage difference between the top and the bottom of the capacitor, and is the voltage difference between the top and the bottom of the capacitor, and 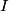 is the clockwise current. This equation must be true for all is the clockwise current. This equation must be true for all 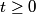 . In particular, at . In particular, at 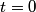 , , 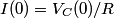 . Since it was already argued that . Since it was already argued that 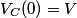 , the voltage of the battery, we must have that , the voltage of the battery, we must have that 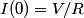 . This means that curves A and B are the only ones that could be correct. We can distinguish between them be solving for the current as a function of time. The current through a capacitor is given by . This means that curves A and B are the only ones that could be correct. We can distinguish between them be solving for the current as a function of time. The current through a capacitor is given by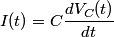 Because of the way we have defined the current 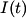 and the voltage and the voltage 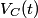 , the right equation is actually , the right equation is actually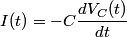 in this case. So, if we differentiate equation (1) and use this relation, we find that 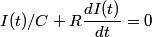 The solution to this differential equation is (with the initial condition 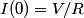 ) )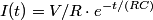 So, the current is 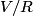 at at 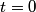 and then it decays exponentially to and then it decays exponentially to 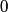 . Thus, answer (B) is the correct. . Thus, answer (B) is the correct. |