Let
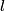 be the length of the string. Then be the length of the string. Then 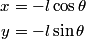 implies that 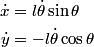 which implies that 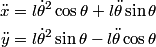 Thus,  So, we need to find 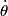 and and 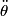 as functions of as functions of 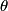 . For . For 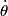 , this can be done by equating the kinetic energy that the mass has when its angle is , this can be done by equating the kinetic energy that the mass has when its angle is 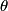 to the change in the mass's potential energy between its initial position and its position when its angle is to the change in the mass's potential energy between its initial position and its position when its angle is 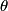 : :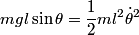 Thus,  In order to find 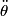 , we use Lagrange's equation , we use Lagrange's equation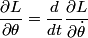 The kinetic energy of the particle is 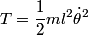 The potential energy of the particle is 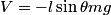 Therefore the Lagrangian of the particle is 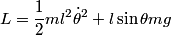 Using Langrange's equation, we find that  Plugging equations (3) and (4) into equation (1)-(2) gives 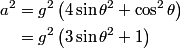 or 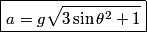 Therefore, answer (E) is correct. |