The wave function corresponding to energy level
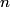 is is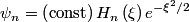 where 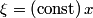 and and 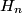 is the is the 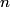 th Hermite polynomial. These wavefunctions represent all possible solutions to the harmonic oscillator potential that go to th Hermite polynomial. These wavefunctions represent all possible solutions to the harmonic oscillator potential that go to 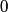 when when 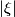 or equivalent or equivalent 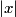 goes to infinity. Therefore, these wavefunctions represent all possuble solutions to the harmonic oscillator potential on a domain that is infinite in at least one direction (like in this problem). Now, Hermite polynomials are even functions if goes to infinity. Therefore, these wavefunctions represent all possuble solutions to the harmonic oscillator potential on a domain that is infinite in at least one direction (like in this problem). Now, Hermite polynomials are even functions if 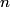 is even and odd functions if is even and odd functions if 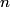 is odd. Therefore, only those is odd. Therefore, only those 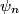 where where 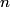 is odd satisfy the boundary condition is odd satisfy the boundary condition 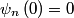 . Therefore, only these . Therefore, only these 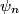 are solutions for the potential in this problem. Therefore, answer (E) is correct. are solutions for the potential in this problem. Therefore, answer (E) is correct. |