The potential energy is
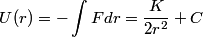 We are told that the potential energy is 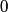 at infinity, therefore we take the constant at infinity, therefore we take the constant 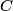 to be equal to to be equal to 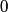 . .The kinetic energy can be found by using the condition 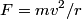 which always holds for circular motion. which always holds for circular motion.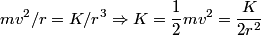 Therefore, the total energy is 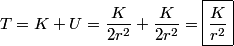 Therefore, answer (E) is correct. |