In order for momentum to be conserved, the thorium nucleus and the helium nucleus must have ``equal and opposite" momenta. The relationship between momentum
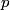 and total energy and total energy 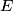 is is 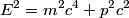 . The kinetic energy . The kinetic energy 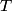 is defined as is defined as 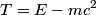 . Therefore, the relationship between momentum and kinetic energy is . Therefore, the relationship between momentum and kinetic energy is 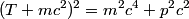 or or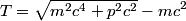 The derivative of 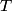 with respect to with respect to 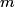 is is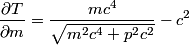 which is always less than 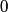 . Therefore, the helium nucleus will have more kinetic energy because it has smaller mass. Therefore, answer (E) is correct. . Therefore, the helium nucleus will have more kinetic energy because it has smaller mass. Therefore, answer (E) is correct. |