Assuming the mass
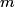 stays exactly on the stays exactly on the 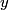 -axis, the force that it feels due to the two -axis, the force that it feels due to the two 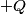 charges is charges is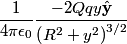 By Newton's Second Law, then 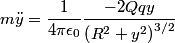 We use the approximation that 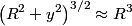 in order to convert this into an equation of motion that gives harmonic oscillations. By analogy with a spring with spring constant in order to convert this into an equation of motion that gives harmonic oscillations. By analogy with a spring with spring constant 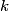 , which has angular frequency , which has angular frequency 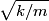 , we have that the angular frequency in this case is , we have that the angular frequency in this case is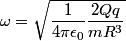 Therefore, answer (E) is correct. |