The angular frequency of a physical pendulum is
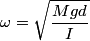 where 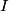 is the moment of inertia about the pivot point and is the moment of inertia about the pivot point and 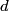 is the distance from the pivot to the center of mass. is the distance from the pivot to the center of mass.If we let 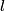 denote the length of the pendulum and denote the length of the pendulum and 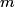 denote the mass of the identical masses, then denote the mass of the identical masses, then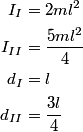 Therefore, 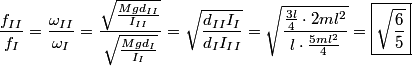 Therefore, answer (A) is correct. |