The general formula for the variance of a random variable
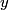 which is a function of which is a function of 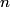 uncorrelated random variables uncorrelated random variables 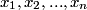 is is ![\begin{align*}\sigma_y^2 = \sum_{i = 1}^n \left[\frac{\partial y}{\partial x_i} \right] \sigma_i^2\end{align*} \begin{align*}\sigma_y^2 = \sum_{i = 1}^n \left[\frac{\partial y}{\partial x_i} \right] \sigma_i^2\end{align*}](../images/1250c216e241d03bfd4ddc878fd6339ea2a779d5.gif) where 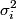 is the variance of the random variable is the variance of the random variable 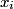 and the partial derivative in brackets is evaluated at and the partial derivative in brackets is evaluated at 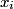 equal to the mean of equal to the mean of 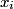 for all for all 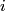 . In this case, . In this case, 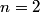 , and , and 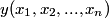 is replaced by is replaced by 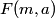 . . 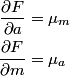 where 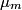 and and 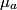 are the means of the measurements of are the means of the measurements of 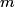 and and  , respectively. Thus, , respectively. Thus,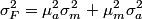 or 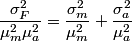 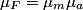 because the measurements are uncorrelated. Therefore, because the measurements are uncorrelated. Therefore,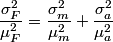 Therefore, answer (C) is correct. |