Let
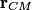 be the position of the center of mass, let be the position of the center of mass, let  be the position of a point on the circumference, and let be the position of a point on the circumference, and let 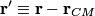 be the position of a point on the circumference with respect to the center of mass. be the position of a point on the circumference with respect to the center of mass.Then, 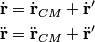 We are told that the cylinder rolls at a constant speed. Therefore, the center of mass is NOT accelerating. Therefore, 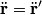 That is the acceleration vector of the particle in the rest frame is the same as the acceleration vector in the center of mass frame. In the center of mass frame, the particle exhibits uniform circular motion, so its acceleration is constant and always direction toward the center of circle (which is also the center of mass). When the particle touches the plane, the center of mass is directly above it, so the acceleration points up. Therefore, answer (C) is correct. |