The coefficient
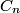 of of 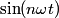 in the Fourier expansion of in the Fourier expansion of 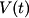 is is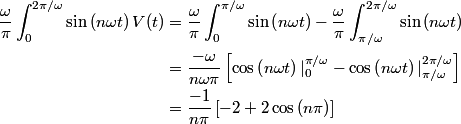 When 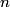 is even is even 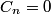 and when and when 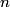 is odd is odd 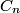 equals equals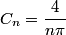 The coefficients 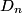 of of 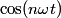 are are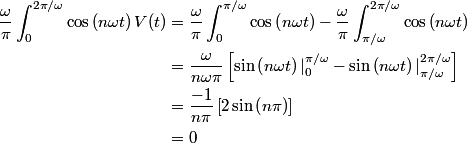 Therefore, the coefficients of 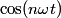 are all zero. are all zero.Therefore, answer (B) is correct. |
The coefficient
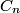 of of 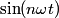 in the Fourier expansion of in the Fourier expansion of 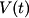 is is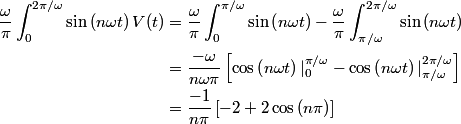 When 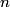 is even is even 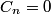 and when and when 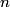 is odd is odd 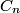 equals equals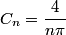 The coefficients 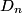 of of 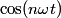 are are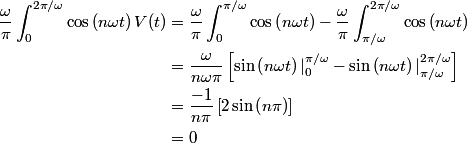 Therefore, the coefficients of 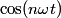 are all zero. are all zero.Therefore, answer (B) is correct. |