We first find the equivalent resistance seen by the battery. Resistors
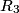 and and 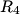 combine to give a combine to give a 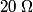 resistor, which combines resistor, which combines 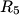 to give a to give a 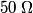 resistor, which combines with resistor, which combines with 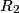 to give a to give a 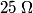 resistor, which combines with resistor, which combines with 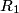 to give a to give a 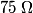 . The current through this equivalent resistor (which is also the current through . The current through this equivalent resistor (which is also the current through 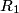 ) is ) is 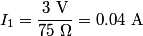 We can find the current through 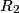 and and 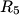 by the current division formula by the current division formula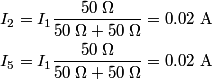 Similarly, the currents through 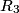 and and 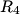 are are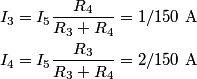 Therefore, the power dissipated by each resistor is 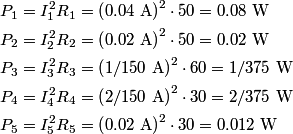 Therefore, resistor 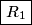 dissipates the most power. Therefore, answer (A) is correct. dissipates the most power. Therefore, answer (A) is correct. |