The eigenstates with
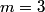 are are 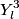 where where 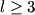 . Therefore, the desired probability is . Therefore, the desired probability is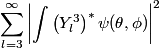 Using the fact that the spherical harmonics are orthogonal and normalized, this reduces to 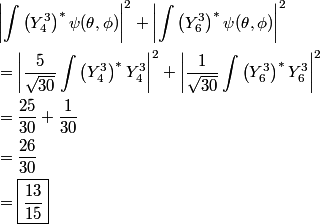 Therefore, answer (E) is correct. |
The eigenstates with
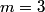 are are 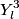 where where 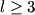 . Therefore, the desired probability is . Therefore, the desired probability is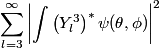 Using the fact that the spherical harmonics are orthogonal and normalized, this reduces to 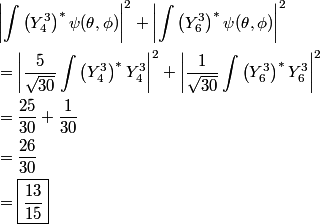 Therefore, answer (E) is correct. |