We will use the fact that
 where  is any complex number. is any complex number. We assume that 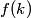 is a Gaussian and that is a Gaussian and that 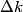 is its standard deviation. Then is its standard deviation. Then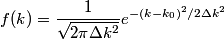 where the prefactor of 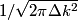 is for normalization. Then, is for normalization. Then, 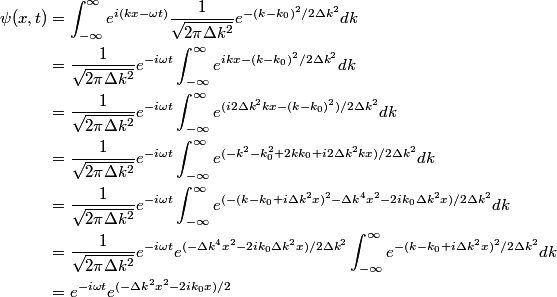 where equation (1) was used to evaluate the integral. This implies that 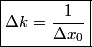 Therefore, answer (B) is correct. |