(A) The efficiency of a Carnot cycle is defined as
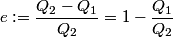 It is well-known that the efficiency is also equal to 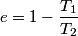 This implies that 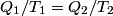 . Thus, answer (A) should not be chosen. . Thus, answer (A) should not be chosen. (B) Because, dS = dQ/T, and the hot reservoir loses heat while remaining at the same temperature, its entropy must decrease. (C) Entropy is a state variable, so it must be the same at the beginning and the end of a cycle. Thus, answer (C) is false, and it should be chosen. (D) By conservation of energy, this must be correct. So, answer (D) should not be chosen. (E) From the formula for the efficiency above, we see that it is only dependent on the temperatures of the hot and cold reservoirs. So, answer (E) should not be chosen. |