We approximate the magnetic field inside the small circular wire as a constant equal to the value of the magnetic field at the center:
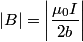 The flux through the small wire is then 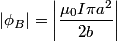 and the time derivative of the flux is then 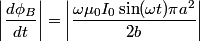 By Faraday's Law in integral form, this is equal to the induced emf in the small loop. Thus, answer (B) is correct. |