Because the fixed point is far from the loop, we can approximate the current loop is an ideal magnetic dipole. The magnetic field due to an ideal magnetic dipole with dipole moment
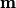 is given by is given by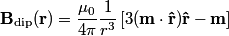 Therefore, if your location relative to the ideal magnetic dipole is held constant, then 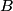 is proportional to the magnetic dipole moment is proportional to the magnetic dipole moment 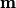 . The dipole moment of a current loop is given by . The dipole moment of a current loop is given by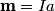 where I is the current in the loop and a is the area of the loop. The area a for a circular loop of radius b is equal to 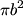 , so the magnetic dipole moment equals , so the magnetic dipole moment equals 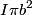 , thus the magnetic field is proportional to , thus the magnetic field is proportional to 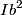 . Hence answer (B) is correct. . Hence answer (B) is correct. |