The only forces on the particle are gravity and the normal force. The normal force acts in a direction orthogonal to the tangential direction. Therefore, it does not contribute to the acceleration. So, we need only find the component of the gravitational acceleration in the tangential direction. The gravitational acceleration is
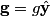 The derivative of 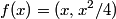 with respect to with respect to  gives a tangent vector: gives a tangent vector: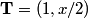 So, the UNIT tangent vector is 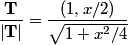 Therefore, the answer is 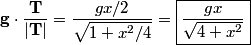 Therefore, answer (D) is correct. |