The potential energy of sphere A when it is released is
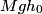 . Therefore its kinetic energy just before it hits sphere B is . Therefore its kinetic energy just before it hits sphere B is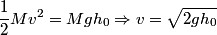 By conservation of momentum, the velocity 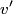 of the conglomerate just after the collision is of the conglomerate just after the collision is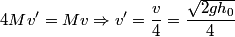 Therefore, the kinetic energy of the conglomerate is 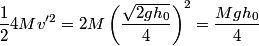 When the conglomerate reaches its maximum height 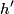 , all of this kinetic energy is converted into potential energy, so , all of this kinetic energy is converted into potential energy, so 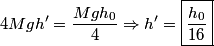 Hence, answer (A) is correct. |